https://leetcode.com/problems/maximum-width-of-binary-tree/

Given a binary tree, write a function to get the maximum width of the given tree. The width of a tree is the maximum width among all levels. The binary tree has the same structure as a full binary tree, but some nodes are null.

The width of one level is defined as the length between the end-nodes (the leftmost and right most non-null nodes in the level, where the null nodes between the end-nodes are also counted into the length calculation.

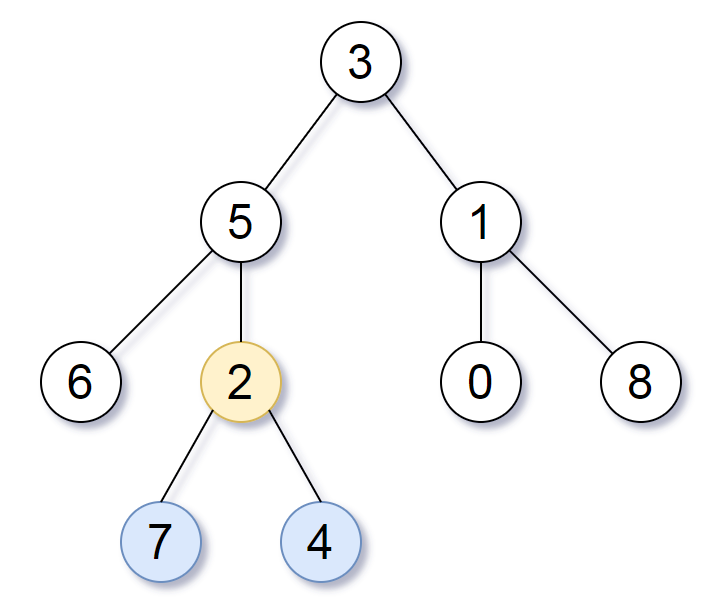
Example 1:

Input: 

           1
         /   \
        3     2
       / \     \  
      5   3     9 

Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).

https://leetcode.com/problems/count-complete-tree-nodes/

Input: 
    1
   / \
  2   3
 / \  /
4  5 6

Output: 6

https://leetcode.com/problems/serialize-and-deserialize-binary-tree/

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Example: 

You may serialize the following tree:

    1
   / \
  2   3
     / \
    4   5

as "[1,2,3,null,null,4,5]"

https://leetcode.com/problems/symmetric-tree/

Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

    1
   / \
  2   2
 / \ / \
3  4 4  3

https://leetcode.com/problems/invert-binary-tree/

Invert a binary tree.

Example:

Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/

Given a binary tree rooted at root, the depth of each node is the shortest distance to the root.

A node is deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is that node, plus the set of all descendants of that node.

Return the node with the largest depth such that it contains all the deepest nodes in its subtree.

Example 1:

Input: [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation:

We return the node with value 2, colored in yellow in the diagram. The nodes colored in blue are the deepest nodes of the tree. The input "[3, 5, 1, 6, 2, 0, 8, null, null, 7, 4]" is a serialization of the given tree. The output "[2, 7, 4]" is a serialization of the subtree rooted at the node with value 2. Both the input and output have TreeNode type.

https://leetcode.com/problems/equal-tree-partition/

Given a binary tree with n nodes, your task is to check if it's possible to partition the tree to two trees which have the equal sum of values after removing exactly one edge on the original tree.

Example 1:

Input:     
    5
   / \
  10 10
    /  \
   2   3

Output: True
Explanation: 
    5
   / 
  10
      
Sum: 15

   10
  /  \
 2    3

Sum: 15

https://leetcode.com/problems/find-elements-in-a-contaminated-binary-tree/

Given a binary tree with the following rules:

1. root.val == 0
2. If treeNode.val == x and treeNode.left != null, then treeNode.left.val == 2 * x + 1
3. If treeNode.val == x and treeNode.right != null, then treeNode.right.val == 2 * x + 2

Now the binary tree is contaminated, which means all treeNode.val have been changed to -1.

You need to first recover the binary tree and then implement the FindElements class:

• FindElements(TreeNode* root) Initializes the object with a contamined binary tree, you need to recover it first.
• bool find(int target) Return if the target value exists in the recovered binary tree.

Example 1:

Input
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
Output
[null,false,true]
Explanation
FindElements findElements = new FindElements([-1,null,-1]); 
findElements.find(1); // return False 
findElements.find(2); // return True 

https://leetcode.com/problems/n-ary-tree-level-order-traversal/

Given an n-ary tree, return the level order traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]

https://leetcode.com/problems/cousins-in-binary-tree/

In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.

Two nodes of a binary tree are cousins if they have the same depth, but have different parents.

We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree.

Return true if and only if the nodes corresponding to the values x and y are cousins.

Example 1:

Input: root = [1,2,3,4], x = 4, y = 3
Output: false

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false

Note:

1. The number of nodes in the tree will be between 2 and 100.
2. Each node has a unique integer value from 1 to 100.